1) 문제 풀이 방법
a. 문제 정의
a. 문제 정의
1) 직원들의 키를 선택/선택X (조합)하여 만들수있는 M을 만들때, 최소 직원의 수
i. 조합/순열, 2진, 멀티플을 확인
ii. 1번 토대로 문제의 그래프를 그려 보기
b. 문제의 복잡도를 계산한다.
i. 2의N승, 3의N승….
c. 메모이제이션 고려
i. 상향식 메모이제이션
1) 루트 노드에서 현재 노드까지 누적된 파라메터의 정답 값을 메모이제이션 하는 경우.
ii. 하양식 메모이제이션
1) 현재 노드에서 리프노드까지 리턴되는 값을 계산하여 여 메모이제이션 하는 경우.
1) Dp 메모이제이션
2) 비트마스킹 메모이제이션
iii. 점화식 설정
§ dp[i][j] = 구하려는 값
§ 함수의 파라메터를 사용하여 dp 파라메터를 결정.
□ 함수의 파라메터가 너무 많으면 효율성이 떨어진다.
□ 함수의 파라메터가 너무 적으면 유망한 노드 자르는 경우 발생.
iv. 효율성 검증
1) 그래프 그려보기
1) 하양식
® 이전 방문한 노드인 경우 리턴 (dp > 0) 효율성 높음 O(N)
2) 상향식
® 이전 방문한 노드인 경우 리턴.
® 현재 dp 값과 파라메터의 값과 비교해서 작거나 큰 경우 리턴.
d. 탐색 방법을 설계한다.
i. Tip
1) 상향식으로 먼저 구현 후 하양식으로 변경 후 메모이제이션 적용
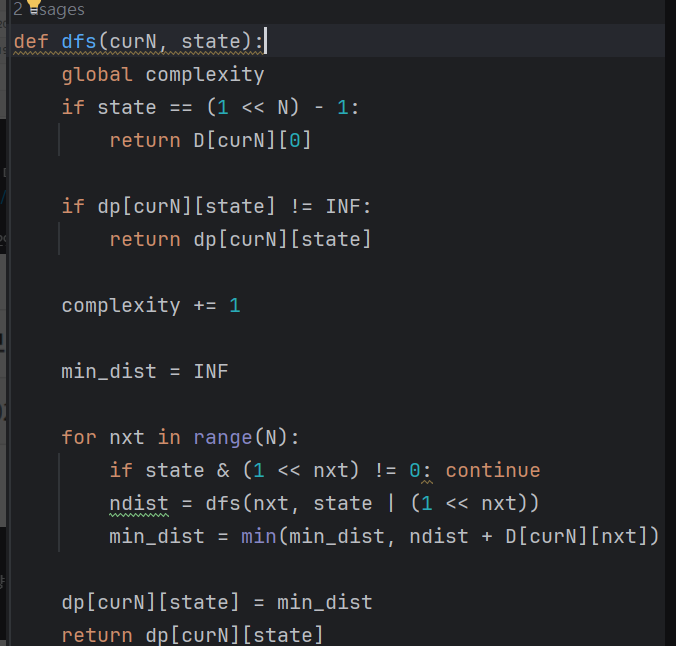
ii. DFS(int index, int cnt) {
iii. DFS(index + 1, cnt + 1);
iv. DFS(index + 1, cnt);
v. }
e. 코드로 효율성 검증.
1) Complex 출력
7) 외판원 순회
https://www.acmicpc.net/problem/16991


a. 문제 정의
a. 문제 정의
1) 외판원 문제, 1번 부터 N번까지 도시를 모두 거쳐서, 다시 원래 도시에 돌아왔을때 가장 적은 비용
i. 순열 멀티플
ii. 그래프 의미 X
b. 문제의 복잡도를 계산한다.
i. N! , 16!
c. 메모이제이션 고려
i. dp 정의
1) dp[i][j] = i번째 도시에서 출발해서, 도시간 조합의 수를 비트마스킹 j 값일때 최소 이동 비용.
ii. 하양식 메모이제이션
1) 현재 노드에서 리프노드까지 리턴되는 누적 거리값을 dp 값을 비교하여 메모이제이션 하는 경우.
1) 비트마스킹 메모이제이션
1) 16! --> 2의 16승
d. 탐색 방법을 설계한다.
cin >> N;
for (int i = 0; i < N; i++) {
for (int j = 0; j < (1 << 16); j++) dp[i][j] = INF;
}
for (int i = 0; i < N; i++) cin >> cx[i] >> cy[i];
for (int i = 0; i < N; i++) { // 도시간 거리 구하기, 배열 형태로 거리 입력
for (int j = 0; j < N; j++) {
if (i == j) continue;
dist[i][j] = sqrt(pow(cx[i] - cx[j], 2) + pow(cy[i] - cy[j], 2));
}
}
double ans = DFS(0, 1);
=========================================================
double DFS(int cur, int mem) {
if (mem == (1 << N) - 1) {
if (dist[cur][0] == 0) return -1;
return dist[cur][0]; // 마지막 돌아가는 이동거리 더해줌
}
if (dp[cur][mem] != INF) return dp[cur][mem];
for (int i = 0; i < N; i++) { // i 다음 방문할 도시
if (dist[cur][i] == 0) continue;
if ((mem & (1 << i)) == (1 << i)) continue;
auto c = DFS(i, mem + (1 << i));
if (c != -1) {
dp[cur][mem] = min(dp[cur][mem], c + dist[cur][i]);
}
}
return dp[cur][mem];
}
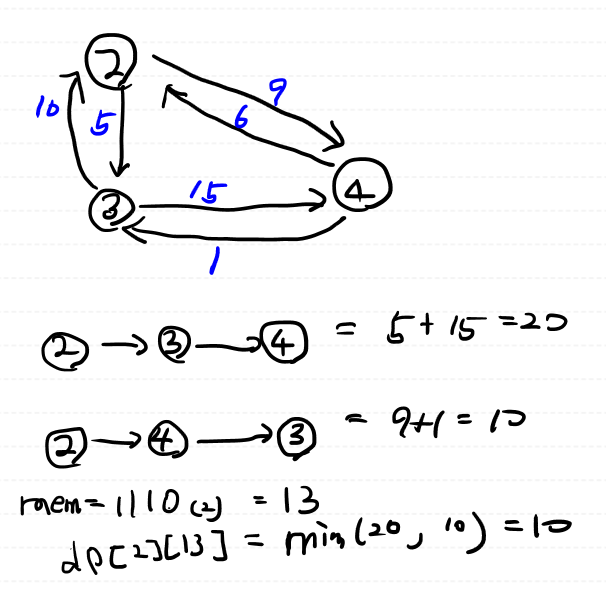
변환 문제
• Swea 요리사 ( 4012 )
○ N <= 16
○ 상향식 -> 하양식 비트마스킹

• Swea 최대상금 1244
○ 상향식 dp 메모이제이션으로 구현.
§
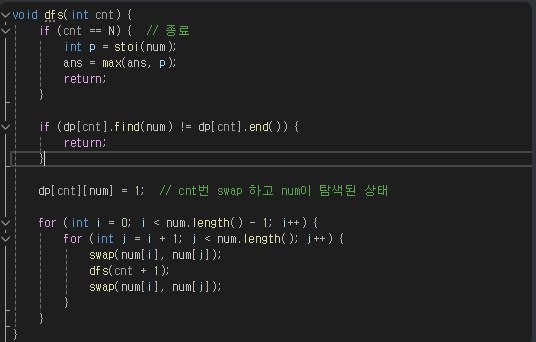
• Swea 부분수열의 합 2817
○ 상향식 -> 하향식 dp 메모이제이션
§
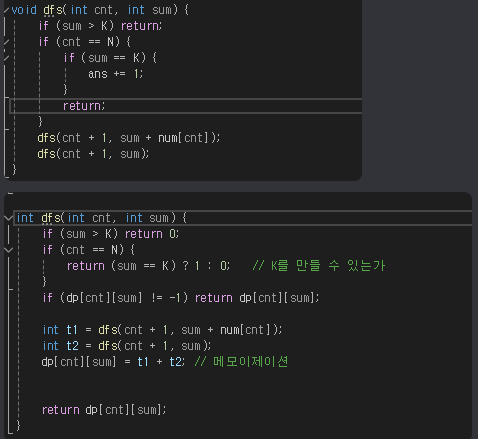
- 1952 수영장 문제
○ 메모이제이션 효과 있나 ( 순열문제 맞음 ?? 아닌것같은데)
○ dp[Index] = sm 만 으로는 유망한 가지를 자름..
○ 리프노드 까지 가봐야 알수있음 -->
§ 하양식
- 3752 가능한 시험점수
○ 냅색으로도 풀어보시길
- ========================================================
- 상향식
○ 1987번: 알파벳 (acmicpc.net)
○

○ 3980번: 선발 명단 (acmicpc.net)
○
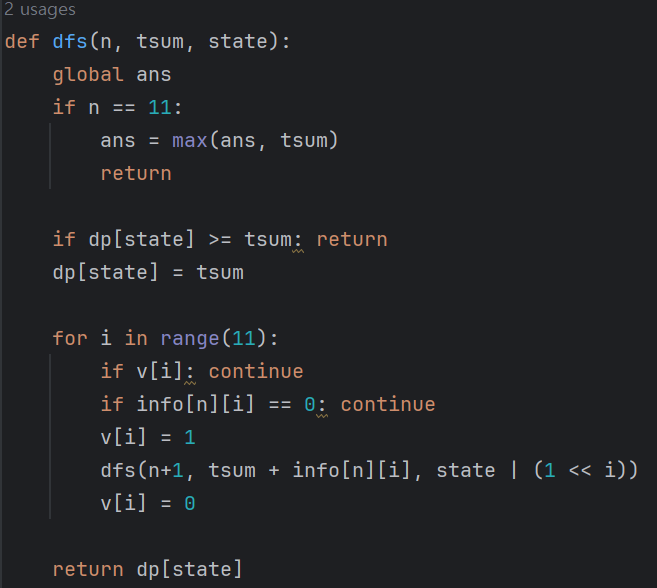
- 게임
○ https://www.acmicpc.net/problem/1103
○

-
- 하양식
○ 1937 욕심쟁이 판다
§ 1937번: 욕심쟁이 판다 (acmicpc.net)

- 16991 외판원순회 3
§ https://www.acmicpc.net/problem/16991
§
- 전기버스
§ SW Expert Academy
§ 5일차
§

'Algorithm' 카테고리의 다른 글
| 2.2 Canvas DrawXX < 나중에 다시 정리 > (1) | 2025.05.07 |
|---|---|
| BackTracking 2 (1) | 2024.06.15 |
| BackTracking 1 (0) | 2024.06.15 |
| Dynamic Programing 4 (0) | 2024.06.15 |
| Dynamic Programing 3 (0) | 2024.06.15 |



