BackTracking 1

백트랙킹 (브루투 포스)
- 모든 경우의 수를 다 탐색해 본다.

1) 그래프 그려 보기
○ 조합 문제.
§ 물건들이 N개, 순서와 상관없고 물건을 뽑았을때 특정 값을 구하는 경우.
□ 특정 값이란 가치의 최대, 최소, 구하는 방법의 개수 등..
§ 물건을 선택하거나, 선택하지 않거나 모든 조합의 경우의 수를 전부 탐색.
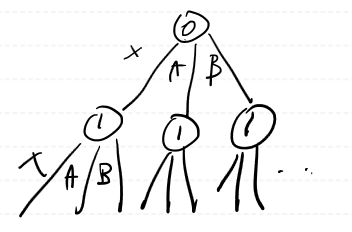
§ 유형 1> 이진 형태
□ 복잡도
® N <= 25 까지 가능, 2의 N승 복잡도 (리프노트)
□ 그래프

□ 코드.

DFS(int index, int cnt) 
{
   if (cnt > M) return; // 가지치기
   if (index == N) // 종료조건, 리프노드
   {
     if (cnt == M) { // 정답갱신 }
     return;
   }
   DFS(index + 1, cnt + 1); // index + 1 번째 물건을 선택하는 경우
   DFS(index + 1, cnt); // index + 1 번째 물건을 선택하지 않는 경우
}

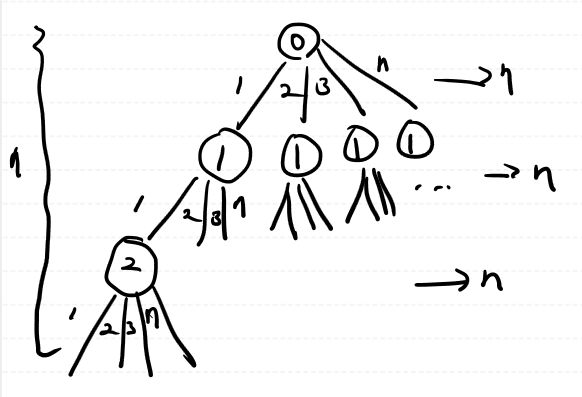
§ 유형 2> 멀티플 형태
□ 복잡도
® N <= 15 까지 가능, 3의 N승 복잡도
□ 그래프
®
□ 코드.

DFS(int index, int cnt) 
{
   ….. (이진형태와 동일)
   DFS(index + 1, ...); // 물건을 선택 안 했을때
   DFS(index + 1, ...); // 물건을 왼쪽에 배치 했을때
   DFS(index + 1, ...); // 물건을 오른쪽에 배치 했을때
}

□
§ 유형 3 > 그래프만 이해하고 사용하지는 말자.
□ 복잡도
® 복잡도 2의 N승 복잡도
- 조합 {1, 2, 3} : {X, 1, 2, 3, 12, 13, 23, 123};
□ 그래프

□ 코드

DFS(-1, 0);
DFS(int index, int sum)
{
  // 매번 정답갱신
  for (int i=index + 1; i<N; i++) 
  {
      DFS(i, sum + arr[i]);
  }
}

○ 순열 문제 (멀티플)
§ 자신이 포함되는 경우 (중복 O)
□ 복잡도
® N <= 8 까지 가능, N의 N승
□ 배열 {1,2,3} 의 모든 순열을 구하여라
® {1,1,1}, {1,1,2}, {1,1,3}…… 3의 3승 총 27가지
□ 그래프

□ 코드

DFS(int cnt)
{
  if (cnt == M) {   // 정답 갱신  return; }
  for (int i=1; i<=N; i++) 
  {
      visit[i] = 1;
      DFS(cnt + 1);
      visit[i] = 0;
  }
}

§ 자신이 포함되지 않는 경우 (중복 X)
□ 복잡도.
□ N <= 11 까지 가능, N! 복잡도
□ 다음 선택에서 이전에 선택한 index를 제외하고 선택한다.
□ Visit 배열에서 체크.
□ 그래프
□ 배열 {1, 2, 3} 대해서 예를 들면)
□ 첫번째 뎁스의 노드는 3번의 탐색, 두번째 뎁스의 노드는 2번의 탐색 ….

□ 코드

DFS(int cnt)
{
  if (cnt == M) {   // 정답 갱신  return; }
  for (int i=1; i<=N; i++) 
  {
      if (visit[i] == 1) continue;
      visit[i] = 1;
      DFS(cnt + 1);
      visit[i] = 0;
  }
}

2) 물건 선택 방법
- 정답 갱신 구간에서 정보를 사용 함.
- Global Visit 배열

int visit[30][30];
DFS(int index, int cnt) 
{ 
   if (cnt > M) return; // 가지치기
   if (index == N) // 리프노드
   {
     if (cnt == M) { // 정답갱신 }
     return;
   }
   visit[index+1] = 1;
   DFS(index + 1, cnt + 1); // index + 1 번째 물건을 선택하는 경우
   visit[index+1] = 0;
   DFS(index + 1, cnt); // index + 1 번째 물건을 선택하지 않는 경우
}

- 레퍼런스로 Local 인자로 넣는 방법

DFS(int index, int cnt, vector<int> &l) 
{
   if (cnt > M) return; // 가지치기
   if (index == N) // 리프노드
   {
     if (cnt == M) { // 정답갱신 }
     return;
   }
   l.push_back(arr[index + 1]);
   DFS(index + 1, cnt + 1, l); // index + 1 번째 물건을 선택하는 경우
   l.pop_back();
   DFS(index + 1, cnt, l); // index + 1 번째 물건을 선택하지 않는 경우
}

- Local 인자로 값 복사하는 경우

DFS(int index, int cnt, string m) 
{
   if (cnt > M) return; // 가지치기
   if (index == N) // 리프노드
   {
     if (cnt == M) { // 정답갱신 }
     return;
   }
   l.push_back(arr[index + 1]);
   DFS(index + 1, cnt + 1, m + tostring(index));
   l.pop_back();
   DFS(index + 1, cnt, m);
}

3) 최적화 과정 진행
3-1) 가지치기
○ 복잡도 계산
§ 최소값 가지치기의 경우 최대 N 100 이하
§ 가지치기 효율성 점검.
□ 정답이 얼마나 빨리 갱신 되느냐
□ 정답에 가까운 값을 얼마나 빨리 내느냐에 따라 성능 결정.
□ 그래프에서 가지치기가 가지마다 많이 적용 되는 경우 --> 가지치기 적용
□ 리프노드 까지 탐색해야 하는 경우가 많은 경우, 효과 적음. --> DP 메모이제이션
○ 가지치기 종류
§ 최소값 가지치기
□ 구하는 값이 최소 값이 경우, 중간 값 계산해서 ans와 비교하여 크면 리턴 (효과 큼 필수)
□ 정답 갱신이 더 잘되는 리커시브 함수를 호출한다.
□ DFS() 재료선택 안하는
□ DFS() 재료선택 하는
§ 최대값 가지치기
□ 구하는 값이 최대 값인 경우, 현재 index 에서 남은것 전부 합해도(total) ans보다 적으면 리턴 (효과 적음)
§ 조건 가지치기
□ 현상태 조건에 의하여 재귀를 실행하지 않음
3-2) DP 메모이제이션
○ 다음 섹션

3) 문제 풀이 방법
a. 문제 정의
i. 조합/순열, 2진, 멀티플을 확인
ii. 1번 토대로 문제의 그래프를 그려 보기
iii. 문제 정의
1) 직원들의 키를 선택/선택X (조합)하여 만들수있는 M을 만들때, 최소 직원의 수
b. 문제의 복잡도를 계산한다.
i. N > 1000, 백트랙킹 불가능(메모이제이션 적용해도 X), DP or 다른 알고리즘 선택
1) N ( child 개수, 가지 수 ), M ( depth )
a) N의 M승
c. 최적화 기법을 선택을 고려한다.
i. N >= 30 이면 DP 메모이제이션 or N <= 30 가지 치기
ii. 상향식 백트랙킹 or 하양식 백트랙킹
iii. DP 정의
1) Dp[i][j] = i 인덱스를 고려했을때, 최대 j의 가치.
d. 탐색 방법을 설계한다.

DFS(int index, int cnt) {
  DFS(index + 1, cnt + 1);
  DFS(index + 1, cnt);
}

유형 1. 조합의 모든 경우 구하기 (이진 트리 형태).

1) 부분 집합 합 구하기 ( N <= 65 )
https://westernriver.tistory.com/12
https://swexpertacademy.com/main/code/userProblem/userProblemDetail.do?contestProbId=AV2b78P6ABoBBASw

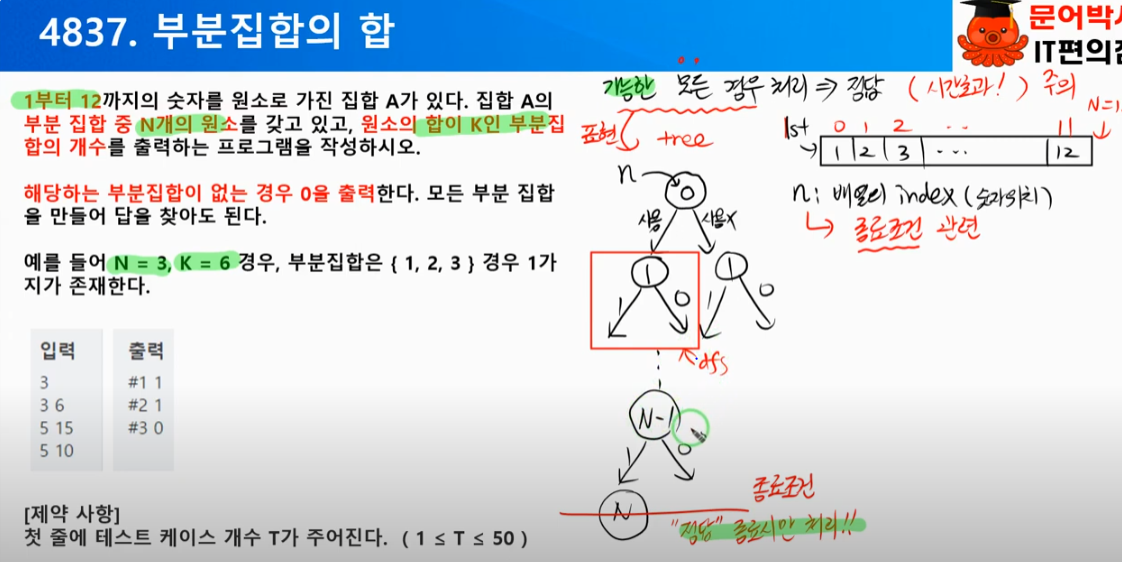
- 문제 정의
- 조합 - 이진형태
- 집합 A에서 N개의 원소를 조합하여, 원소의 합이 S인 부분집합의 개수를 구하여라
- 복잡도
- 2의N승 ( N <= 65 ) 2의65승 > 1억 --> 최적화 필요 https://westernriver.tistory.com/12

- 최적화 기법 고려
- Sum 가지치기를 하면 최적화 효율이 정말 좋음.
○ (거의 대부분 모든 노드들이 가지치기 됨.)
- 탐색 방법 설계
- int DFS(int index, int sum) {
if (sum > W) return 0;

if (index == N) {
if (sum == W) return 1;
return 0;
}
int count = 0;
count += DFS(index + 1, sum + S[index]);
count += DFS(index + 1, sum);
return count;
}

2) 장훈이의 높은 선반 ( N <= 20 )
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AV2b7Yf6ABcBBASw

- 문제 정의
- 조합, 이진
- 점원들의 키를 조합하여, B높이 이상을 만들었을때, 가장 B에 가까운 값은 (sum of 키의 최소 값)
• 복잡도
- 복잡도 2의N승 ( N <= 20 ) --> 최적화 필요 없음.
- 최적화 기법 고려
- 탐색 방법 설계

void DFS(int index, int sum) {
if (index == N) {
if (sum >= B) {
ans = min(ans, sum - B);
}
return;
}
DFS(index + 1, sum + S[index]);
DFS(index + 1, sum);
}

3. 배열의 최소 합 (N <= 10) (4881)
https://swexpertacademy.com/main/learn/course/lectureProblemViewer.do
https://glory-summer.tistory.com/82

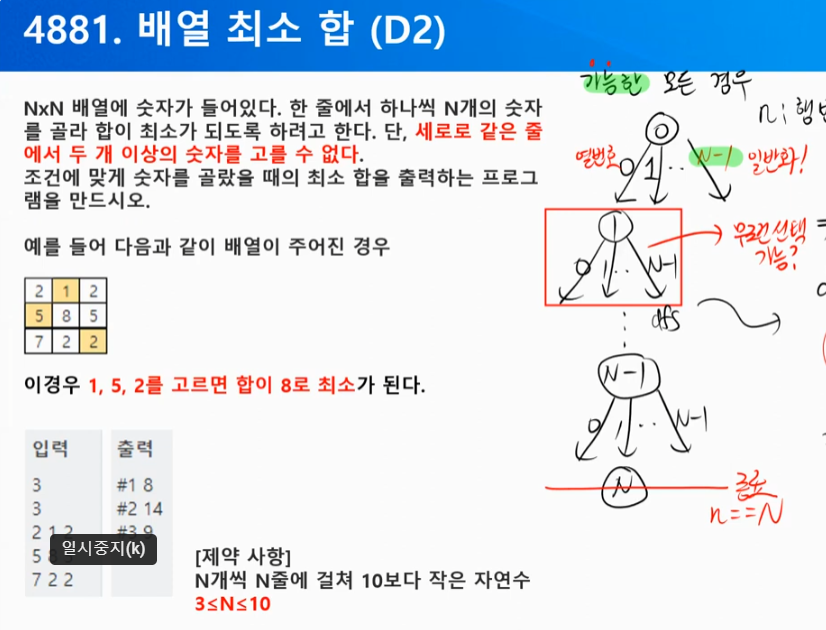
- 문제 정의
- 조합, 멀티플
- i행 j행의 숫자를 골랐을때 (세로같은 줄 X), 최소 합을 구하여라.
• 복잡도
- 자기 자신 포함하지 않는 순열 N! ( N <= 10 ) --> 최적화 필요 없음.
- 최적화 기법 고려
- 탐색 방법 설계

4. 최소 생산 비용
https://swexpertacademy.com/main/talk/solvingTalk/boardCommuView.do?commuId=AWrmdCqqQeYDFARG

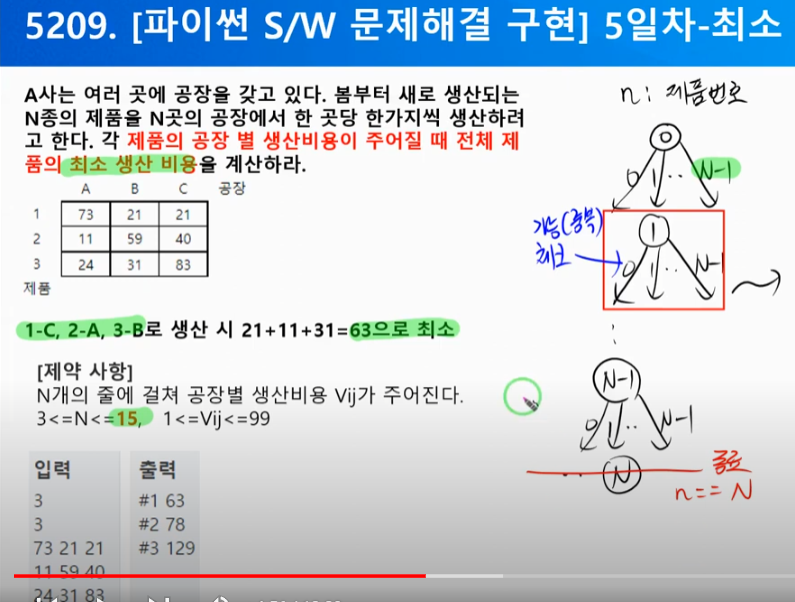
문제 정의
- 순열, 멀티플
- i행 j행의 공장과 제품를 골랐을때, 최소 생산 비용을 구하여라
• 복잡도
- 자기자신 포함하는 순열 ( N <= 15 ) --> 15의 15승 --> 최적화 필요
- 최적화 기법 고려
- 생산 비용의 값에 따라 대부분 모든 가지들에 적용됨. --> 최소값 가지치기 적용
- 탐색 방법 설계
- 가지치기 조건
○ If (ans > sum) return;
- 3번 문제와 동일

5. 전기버스2 (5208)
https://independenceday.tistory.com/entry/SWEA-5208-%EC%A0%84%EA%B8%B0%EB%B2%84%EC%8A%A42

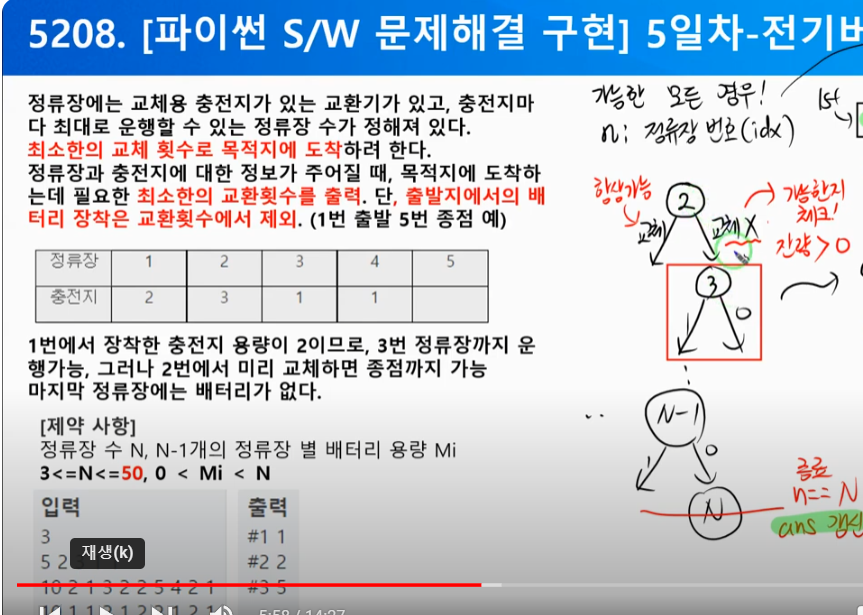
문제 정의
- 조합, 이진
- 정류장 마다 충전지를 교환(0), 교환(X), 최소 충전지 교환횟수.
• 복잡도
- N <= 100, 2의 100승 --> 최적화 필요.
- 최적화 기법 고려
- 최소값 가지치기
○ 교환횟수가 정답 갱신이 되면, 모든 가지들이 다 적용 될수 있음. (효과 좋음)
- 교체하지 않는 DFS를 교체하는 DFS보다 먼저 호출한다
- 탐색 방법 설계

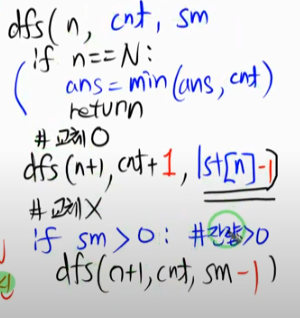
6. 2819. 격자판의 숫자 이어 붙이기

문제 정의
- 순열, 멀티플 4진
- 동서남북으로 이동하면서 만들수 있는 7자리의 개수
• 복잡도
- 4의 N승, 4의 7승
- 최적화 기법 고려
- 가지치기 필요 없음.
- 탐색 방법 설계
void DFS(int y, int x, string str) {
if (7 == str.size()) {
//cout << " str : " << str << endl;
s.insert(str);
return;
}

for (int i = 0; i < 4; i++) {
int ny = y + dy[i];
int nx = x + dx[i];
if (ny < 0 || ny >= N || nx < 0 || nx >= N) continue;
DFS(ny, nx, str + to_string(pan[ny][nx]));
}
}

7. 사랑의 카운셀러 (1494)
https://swexpertacademy.com/main/code/problem/problemDetail.do

8. 가능한 시험 점수 (3752)
https://swexpertacademy.com/main/solvingProblem/solvingProblem.do

'Algorithm' 카테고리의 다른 글

BackTracking 3 (1)	2024.06.15
BackTracking 2 (1)	2024.06.15
Dynamic Programing 4 (0)	2024.06.15
Dynamic Programing 3 (0)	2024.06.15
Dynamic Programing 2 (0)	2024.06.15

SimonLee Graphic Story

BackTracking 1

'Algorithm' 카테고리의 다른 글

티스토리툴바

BackTracking 1

'Algorithm' 카테고리의 다른 글

관련글

티스토리툴바