문제의 예제와 풀이방법은 문어박사 youtube를 참조해서 작성함.
DP 문제 풀이 순서
1) 복잡도 확인하기
1-1) DP 메모이제이션
- N <= 50 or 100
- 복잡도 계산하는 방법은 조건 마다 다르다.
§ 이진(2의N승), 삼진(3의N승), 사진(4의N승)
- 복잡도를 계산하면 엄청 크지만, 중복이 그만큼 많이 되는 경우 가능.
1-2) 일반 DP
- N(아이템 개수) * M(조건 크기) < 최대 1억, 천만 이하 적정.
1-3) 냅색DP
- 최대 N = 10만, M = 100
- N이 큰 경우는 알고리즘을 통해 줄이자.
• 복잡도 종류
- 메모리 : N * M bytes
- 중첩 For 문 : N * M
2) DP 유형 판별하자.
- 풀어본 유형은 바로 점화식을 세울수 있음.
2-1) 이전 or 이후 dp값을 참조하여 값을 계산하는 경우.
○ 금화 모의, 숫자판 놀이 (위-아래, 아래-위)
○ 집합에서 K개 선택하기 (이항계수, 옆)
○ 최대 정사각형
2-2) 특정한 경우, 경로의 개수 구하는 문제
2-3) 값을 만들수 있는지 여부가 중요한 경우.
○ 저울 문제 (현재 3k추를 가지고 5kg추를 만들기 위해서는 2kg추가 만들수 있어야 한다. 냅색)
2-4) 최장 공통 부분서열(LCS, Global Alignments)
○ 두 문자열 공통 부분문자열의 길이 구하기
○ LCS[i][j] = A문자열 Ai, B문자열 Bi 경우, 최대 공통부분 서열 길이
○ Global Alignments
2-5) 동전 거스름돈 (냅색) - 그리디와 응용
○ 0, 1 문제 (조합)
2-5) 개수 구하기 (X) 완전 정보게임, 제한된 비트스트링의 개수 구하기
3) 부분 문제 정의 하기
3-1) DP 정의하기
a. DP[….][….] = 구하려는 값으로 정의하기 < 가장 중요 !!! >
b. 파라메터 정하기
i. 1차원 DP
1) Dp[i] = i번째 물건을 고려했을때, 최대 or 최소 or 경로의 개수
ii. 2차원 DP
1) M이 구체적으로 주어지면 해당 값을 배열 크기로 dp 테이블을 설정한다.
a) int dp[1001][1001];
2) M이 구체적으로 주어져 있지 않는 경우, 문제의 조건을 가지고 M을 정의한다.
a) Dp 테이블 1차원으로 풀수있을까 ? No
b) 해당 조건을 가지고 M을 정의한다.
i) RGB 문제
iii. 다차원 DP
1) 문제의 조건 혹은 아이템 선택시 종속적인 (독립X) 것들이 차원으로 됨.
c. 메모리 제한 확인하기
i. 100MB, 512MB 제한 걸려 있음.
ii. DP[100,000][100] : 10MB
3-2) 부분 문제 생각해보기
○ 하양식으로 부분문제 생각하기
i. 이전 DP 값 구해보기
□ 냅색 계열, lcs
® 조건에 대해서 부분문제 생각하기
◊ 현재 값에 선택을 하거나, 선택을 하지 않는 경우에 대해서 생각
□ 일반 경우.
- 두칸 아래 계단을 밟고 현재 계단을 밟는 경우 : dp[i-2]
- 바로 이전 i-1 숫자를 골랐던 경우 : dp[i-1]
- 숫자판 윗행의 j-1, j, j+1 열 해당하는 칸 : dp[j-1], dp[j], dp[j+1]
ii. 연산관계를 적용
1) 최대 또는 최소를 구하여라 : max, min
2) 경로의 개수를 구하여라 : sum
3) 만들수 있는지 / 없는지 : 1 or 0
○ 상향식으로 부분문제 생각하기
i. 바로 다음의 상황을 다 구해보기
§ 구현
□ Dp[i+1][j] = dp[i][j]
4) DP 설계 (손 작성)
4-1) 기저 조건 세우기
i. 초기값 설정 : DP[1] = 0; DP[2] = 0
ii. 점화식에서 i-1, i-2 식이 있는 경우, 음수가 되지 않는 i = 2까지 기저조건을 구해주면 된다.
iii. 기저조건이 필요없는 경우가 있음.
1) Ex) 점화식에 i-1가 있는 경우, dp[1] 까지 기저를 구할텐데, for (i=1 이 가능하면 ) 기저 조건 생략가능.
iv. 2차원 dp의 경우, 배열 형태로 초기화도 가능하다 for (int i=0; i<N; i++) dp[i] = 0;
4-2) 반복문을 사용하여 점화식 구현 (1차원, 2차원)
i. Int DP[N+ 1] 크기를 갖도록 하고 index 1 부터 시작하는 것이 편함. (1번째 물건)
ii. DP 계산할때 조건이 있는 경우가 많음.
1) 각 조건 마다 dp update
iii. 일렬 가는 부분 (금화모의, 냅색), 대각 행렬 (팰린드롬)
4-3) 개수를 구하는 경우
§ 기저 값을 설정 Dp[0][0] = 1
§ Dp 값을 더해 나간다.
□ Ex) dp[i][j] += dp[i-1][j];
5) DP 테이블 작성. (손 작성 - Print 체크)
문제 푸는 방법 정리
1. 복잡도 확인하기
2. DP 유형 확인하기
3. 부분문제 정의하기 ( Dp[i] = ?, 하양식, 이전 DP 값)
4. DP 설계하기 (기저값, 점화식 구현 )
5. DP 테이블 작성하기
문제 풀기
유형1) 이전합을 사용하여 현재 DP 구하기 1차원
1) 피보나치 풀어보기
https://www.acmicpc.net/problem/2747

n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
1.복잡도 확인하기
- N <= 45
2. DP 유형 확인하기
- 이전 인덱스를 참조하여 값을 계산 경우
3. 부분문제 정의하기
- DP[i] = i번째의 피보나치 수
- 일반화 : 상향식
- n-1번째 피보나치의 수, n-2번째 피보나치의 수
- 연산 : 합
4. DP 설계
- 기저조건 : dp[0] = 0, dp[1] = 1, dp[2] = 1, dp[3] = dp[1] + dp[2]
- 점화식 구현 : dp[i] = dp[i-2] + dp[i-1]; (조건X)
5. DP테이블 작성
2) 1로 만들기
https://www.acmicpc.net/problem/1463

1. 복잡도 확인하기
- N = 1,000,000(백만) 1차원 가능
2. DP 유형 확인하기
- 값을 만들수 있는지 여부로 연산하는 경우
3. 부분문제 정의하기
- dp[i] = 구하려는 수i를 1로 만들때 최소 연산횟수
- 하양식
○ 이전 DP 값 : dp[N / 3], dp[N / 2], dp[N - 1]
- 연산 : min
4. DP 설계
- 기저값 : d[1] = 0; d[2] = 1; d[3] = 1;
- 점화식 구현 (조건 있음)
d[i] = d[i - 1] + 1;
if (i % 3 == 0) d[i] = min(d[i], d[i / 3] + 1);
if (i % 2 == 0) d[i] = min(d[i], d[i / 2] + 1);
5. DP 테이블
3) 연속합 ( 다시 정리)
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.
예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다
https://www.acmicpc.net/problem/1912
1. 복잡도 확인하기
- n ≤ 100,000
2. DP 문제유형
- 하양식
3. 부분문제 정의하기
- DP[i] = i번째 숫자를 고려했을때, 최대 연속된 수열의 합
- 하양식
○ 이전 DP 값 : dp[i-1], dp[i]
○ 추가하는 경우 dp[i] = dp[i-1] + s[i]
○ 추가하지 않는 경우, 다시 새로 시작 dp[i] = s[i]
4. DP 설계
- 기저조건
○ dp[1] = 1;
- 점화식 구현
○ d[1] = s[1];
○ for (int i = 2; i <= N; i++) {
○ d[i] = max(d[i-1] + s[i], s[i]);
○ }
3) 1,2,3 더하기
https://www.acmicpc.net/problem/9095
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
• 1+1+1+1
• 1+1+2
• 1+2+1
• 2+1+1
• 2+2
• 1+3
• 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.

1. 복잡도 확인하기
- N <= 11
2. DP 유형 확인하기
- 이전 인덱스를 참조하여 값을 계산 경우
3. 부분문제 정의하기
- dp[i] = 숫자i를 1,2,3의 합으로 만드는 방법의 수
- 하양식
○ 이전 dp 값 : dp[i-1], dp[i-2], dp[i-3]
4. DP 설계
- 기저값 : dp[1] = 1, dp[2] = 2, dp[3] = 4 ( 경우의 수를 다 써보자 )
- DP 구현
○ d[1] = 1; d[2] = 2; d[3] = 4;
○ for (int i = 4; i <= N; i++) {
○ d[i] = d[i - 1] + d[i - 2] + d[i - 3];
5. DP 테이블
4) 계단 오르기
https://www.acmicpc.net/problem/2579
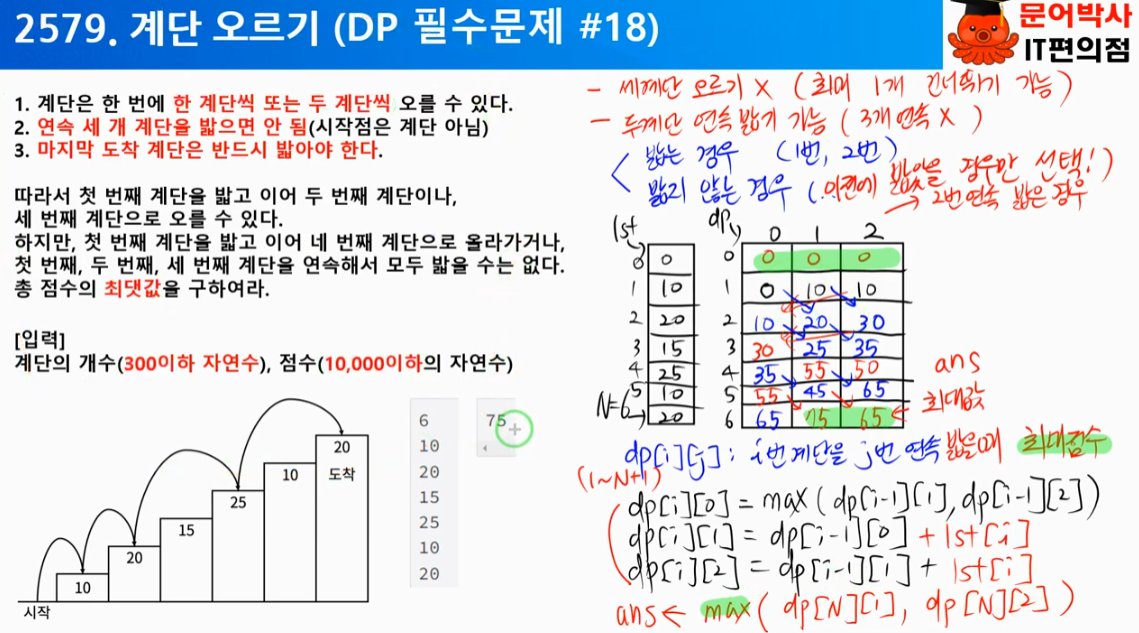
1. 복잡도 확인하기
- N <= 300
2. DP 유형 확인하기
- 이전 인덱스를 참조하여 값을 계산 경우
3. 부분문제 정의하기
- D[i] = i번째 계단을 밟았을때 총 점수 최대 값
- 하양식
○ 이전 dp값 : dp[N-1], dp[N-2], dp[N-3]
- 연산 : 합, max
4. 점화식 설계 :
- 초기값 : D[0] = 0; D[1] = S[1]; D[2] = S[1] + S[2];
- 점화식 구현 : For (i = 3 ~ ) 점화식 사용
- for (int i = 3; i <= N; i++) d[i] = max(d[i - 2] + s[i], d[i - 3] + s[i - 1] + s[i]);
5. DP테이블 :
유형 2. 이전합을 사용하여 현재 DP 구하기 2차원
5) 이동하기 ( 금화 모의 유형, 숫자판 놀이 )
https://www.acmicpc.net/problem/11048
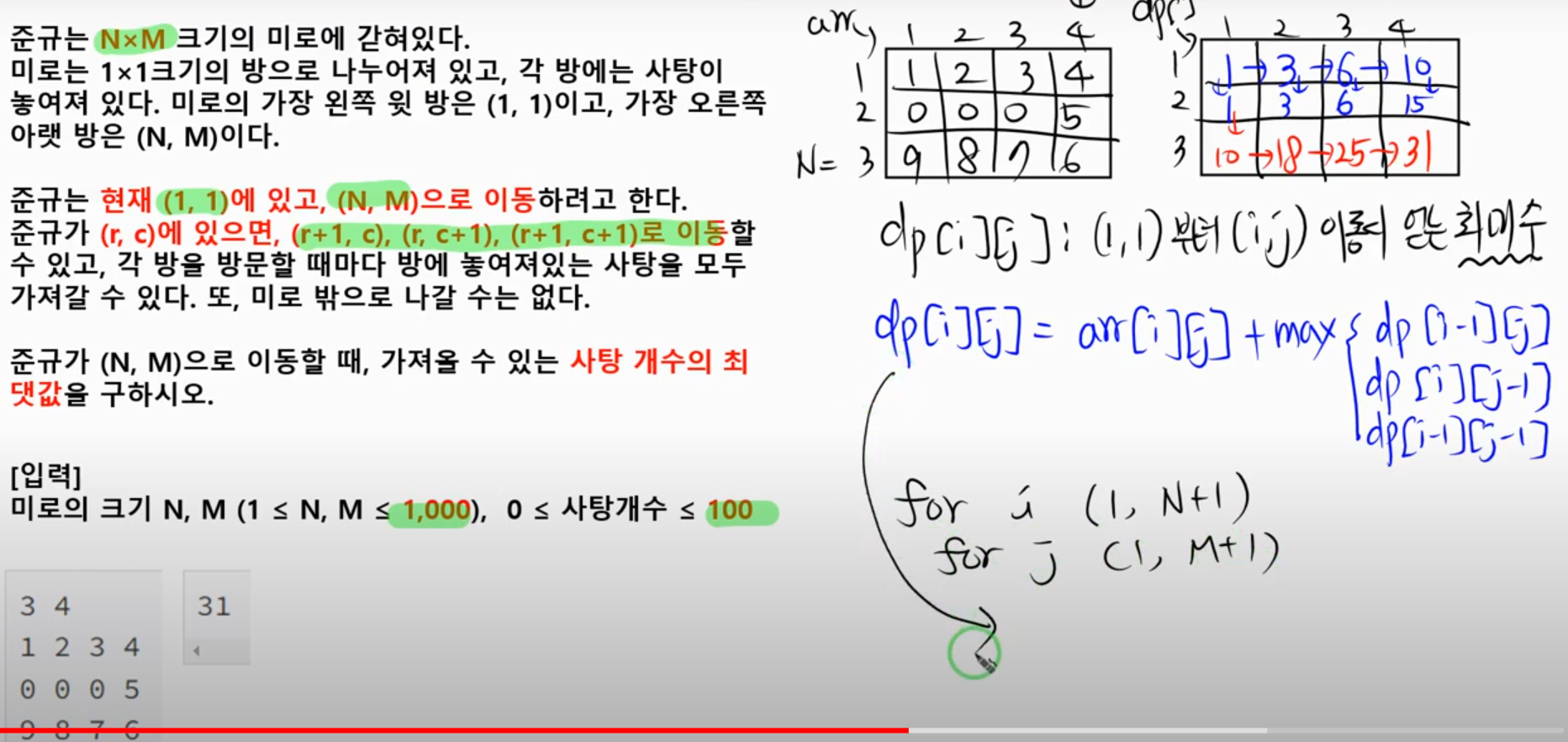
1. 복잡도 확인하기
- N, M <= 1000 ( 1000 * 1000 = 1000000 (백만) ) <-- 2차원 가능.
2. DP 유형 확인하기
- 이전 인덱스를 참조하여 값을 계산 경우
3. 부분문제 정의하기
- Dp[i][j] = i,j 방에 있을때, 최대 사탕의 개수
- 이전 DP 값 : dp[N-1][M], dp[N][M-1], dp[N-1][M-1]
- 연산 : max
4. DP 설계
- 기저값 : 필요없음.
- DP구현:
- for (int i = 1; i <= N; i++) {
- for (int j = 1; j <= M; j++) {
- d[i][j] = max(d[i][j - 1], d[i - 1][j]);
- d[i][j] = max(d[i][j], d[i - 1][j - 1]) + candy[i][j];
- }
5. DP 테이블

6) RGB 거리
https://www.acmicpc.net/problem/1149

1. 복잡도 확인하기
- N * M = N = 1000 * M = 3 < 1억이하. (2차원 가능)
2. DP유형 확인하기
- 이전 인덱스를 참조하여 값을 계산 경우
3. 부분문제 정의하기
- DP[i][j] = i번째 집일 경우, j (0 == R, 1 == G, 2 == B) 페인트 칠할 경우 비용의 최소값
○ N번째 집이 3가지 중 하나의 페인트를 칠할 경우 비용의 최소값?
○ 파라메터 추가해야 겠구나. (0 == R, 1 == G, 2 == B)
- 이전 DP 값 : D[i-1][0], D[i-1][1], D[i-1][2]
- 연산 : min
4. DP 설계
- d[1][0] = s[1][0]; d[1][1] = s[1][1]; d[1][2] = s[1][2]; // 기저
- DP 구현
- for (int i = 2; i <= N; i++) {
- d[i][0] = min(d[i - 1][1], d[i - 1][2]) + s[i][0];
- d[i][1] = min(d[i - 1][0], d[i - 1][2]) + s[i][1];
- d[i][2] = min(d[i - 1][0], d[i - 1][1]) + s[i][2];
- }
- int ans = min(min(d[N][0], d[N][1]), d[N][2]);
5. DP 테이블 구현.

유형 3. 개수 구하기
6) 점프 ( 금화 모의 유형, 숫자판 놀이 )
https://www.acmicpc.net/problem/1890

1. 복잡도 확인하기
- 100 * 100 <= 10000
2. DP 문제유형 확인하기
- 값을 만들수 있는지 여부로 연산하는 경우
3. 부분문제 정의하기
- dp[i][j] = (0, 0)에서 시작하여 i, j로 오는 경로의 수
- 상향식
○ 이후 dp 값 : dp [i + arr[i][j]][j] , dp[i][j + arr[i][j]]
○ 연산 : sum
4. DP 설계
- 기저값 = d[1][1] = 1;
- dp 구현 (조건O)
- for (int i = 1; i <= N; i++) {
- for (int j = 1; j <= N; j++) {
- if (s[i][j] == 0) continue;
- if (d[i][j] <= 0) continue;
- if (nexti <= N) d[i + s[i][j]][j] += d[i][j];
- if (nextj <= N) d[i][ j + s[i][j]] += d[i][j];
- }
- }
5. DP 설계

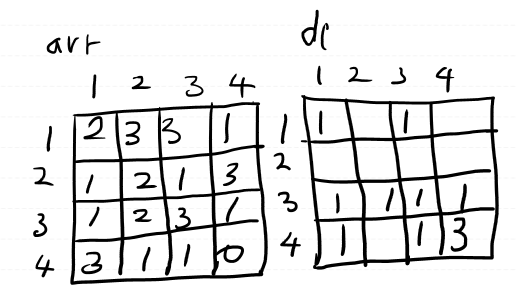
6) 동물원
동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지
https://www.acmicpc.net/problem/1309
1. 복잡도 확인하기
- N <= 100000 (십만) 1차원 가능, 2차원 M 몇까지 ?
2. DP 문제유형
- 이전인덱스를 참조하여 값을 계산하는 경우
3. 부분문제 정의하기
- D[i][0] = 현재 사자를 i번째 열에 배치하지 않는 경우
- D[i][1] = 현재 i번째 열 첫 번째칸 우리에 사자를 배치하는 경우
- D[i][2] = 현재 i번째 열 두 번째칸 우리에 사자를 배치하는 경우
- 이전 DP 값 : dp[i-1][0], dp[i-1][1], dp[i-1][2]
- 연산 : sum
4. DP 설계
- 기저 설계
○ d[1][0] = 1; d[1][1] = 1; d[1][2] = 1;
- DP 구현.
○ for (int i = 2; i <= N; i++) {
○ d[i][0] = (d[i - 1][0] + d[i - 1][1] + d[i - 1][2]) % 9901;
○ d[i][1] = (d[i - 1][0] + d[i - 1][2]) % 9901;
○ d[i][2] = (d[i - 1][0] + d[i - 1][1]) % 9901;
○ }
○ int ans = d[N][0] + d[N][1] + d[N][2];
5. DP 테이블
'Algorithm' 카테고리의 다른 글
| BackTracking 2 (1) | 2024.06.15 |
|---|---|
| BackTracking 1 (0) | 2024.06.15 |
| Dynamic Programing 4 (0) | 2024.06.15 |
| Dynamic Programing 3 (0) | 2024.06.15 |
| Dynamic Programing 2 (0) | 2024.06.15 |



