Line, Plane 간 Angle을 구해봅시다.
삼각함수를 사용하여 각도를 계산하는데,
삼각함수에서 사용하는 세타 값은 호도법을 사용한 각도 이므로, 이를 육십분법으로 변환하는 과정이 필요합니다.
그래서 호도법에 대해서 먼저 알아야 합니다.
호도법은 원의 호를 사용하여 각도를 표시하는 방법입니다.

변환하는 과정만 알면 되므로 이를 코드로 변환하면 다음과 같습니다.
라디안 --> 디그리(도) 변환시 사용
- 1 rad = (180 / 파이)
디그리(도) --> 라디안 변환시 사용
- 1 degree = (파이 / 180)
public static float DegreeToRadian(float angle)
{
return angle * ((float)Math.PI / 180.0f);
}
public static float RadianToDegree(float theta)
{
return theta * (180.0f / (float)Math.PI);
}
Line과 Line 사이의 각도를 알기 위한 식은 내적 공식을 사용 합니다.
분자 부분의 작대기는 절대 값이고, 분모 부분은 norm(벡터의 크기) 입니다.

Line A, Line B의 방향벡터가 공식의 A, B로 들어가면 됩니다.
여기서 방향벡터, 노멀벡터, 법선벡터 모두 같은의미 이며,
위 벡터의 특징은 크기는 상관이 없고 방향만 의미가 있습니다.
A, B벡터는 노멀라이즈 과정을 거쳐야 하며, 단위 벡터가 됩니다.
단위 벡터의 크기는 항상 1 입니다.
1) Line vs Line
오른 손의 법칙에 의해 엄지가 위를 향한 상태에서 AB 벡터에서 CD 벡터의 값이 구해 집니다.

AB 벡터 CD 벡터의 각도는 범위는
B방향에서 C 방향이 아닌 D가 있는 방향입니다.
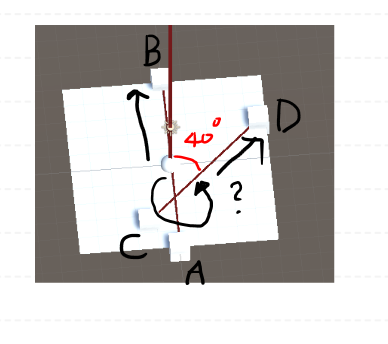
이것도 B 방향에서 D방향이니 40도가 나옵니다.
그러면 B방향에서 C방향으로 320도는 어떻게 구할까요 ?
먼저 절대값을 취한 이유부터 생각해 봅시다.
f`(x) = y 역함수는 동일한 x값에 따라 하나의 해만 존재 해야 합니다.
아크 코사인 값이 절대값을 취하면 아래 그림의 빨간 영역에 해당이 되는데,
0 ~ 파이/2 구간을 제외하고는 그래프가 대칭이 되어 역함수의 해가 여러개가 나오기 때문에 해에서 제외 됩니다.
그래서 모든 y 값에 대해서 x 값은 항상 90도 이하의 값이 나오게 됩니다.

내가 사이각을 구할때 벡터의 방향과 상관없이
두 직선이 교차했을때 가장 작은 예각 ( < 90도 )을 구하기 위해서는 <공식1>에 절대값을 적용하면 됩니다.
그림 2의 처럼 0 ~ 360각도를 구하기 위해서는 어떻게 할까요 ?
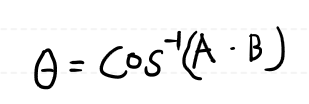
먼저 절대값을 식에서 제거해 줍니다.
절대값을 그래프는 x = 파이 기점으로 대칭이 됩니다.

두 직선이 교차했을때 각이 (0 <180도)가 구해 집니다.
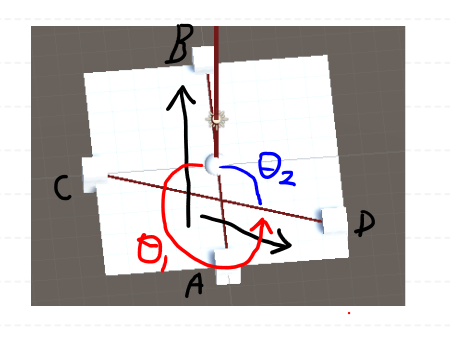
세타 2에 해당하는 각도는 105도가 구해집니다.
세타 1에 해당하는 각도를 알기 위해서는 360에서 세타2를 빼주면 됩니다.
360을 빼주는 경우는 삼중곱을 통해서 알 수 있습니다.
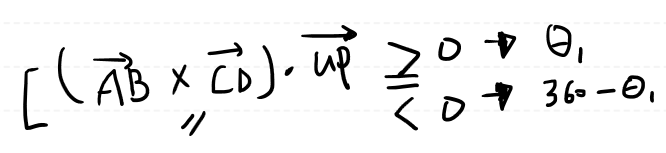
외적을 통해서 AB벡터와 CD벡터의 노멀벡터의 방향, 즉 오른손의 법칙을 적용하면
위 방향을 가리키는 노멀벡터가 나올 것이며,
Up 벡터와 내적을 하게되면, 결국 동일한 Up Vector와 내적을 하는 것이며,
그 값은 내적 공식에 의해 1이 나오게 됩니다.
그림 3은 노멀벡터의 방향이 오른손의 법칙에 의해 아래쪽을 향하게 되고,
360 - 세타 1에 해당하는 각도가 나 올 것 입니다.
2) Plane vs Line
Plane의 노멀벡터가 공식의 A
Line의 방향벡터가 공식의 B 들어가면 됩니다.
Plane의 경우 게임엔진에서 up vector 를 사용하시면 됩니다.

3) Plane vs Plane
각 Plane의 노멀벡터가 공식의 A, B에 들어가면 됩니다.

코드는 다음과 같습니다.
public float AnglePlanes(Plane p1, Plane p2)
{
var dot = Vector3f.DotProduct(p1.GetNormal(), p2.GetNormal());
float theta = (float)Math.Acos(Math.Abs(dot));
return RadianToDegree(theta);
}
public float AngleLinePlane(Line3d l1, Plane p1)
{
var dot = Vector3f.DotProduct(l1.GetDirection(), p1.GetNormal());
float theta = (float)Math.Acos(Math.Abs(dot));
float angle = RadianToDegree(theta);
return 90 - angle;
}
public float AngleLine3D(Line3d l1, Line3d l2)
{
var dot = Vector3f.DotProduct(l1.GetDirection(), l2.GetDirection());
var cross = Vector3f.CrossProduct3D(l1.GetDirection(), l2.GetDirection());
float theta = (float)Math.Acos(dot);
var angle = RadianToDegree(theta);
if (Vector3f.DotProduct(new Vector3f(0f, 1f, 0f), cross) >= 0)
{
return angle;
}
return 360 - angle;
}
public float AngleLine2D(Line2d l1, Line2d l2)
{
var dot = Vector3f.DotProduct(l1.GetDirection(), l2.GetDirection());
float theta = (float)Math.Acos(Math.Abs(dot));
return RadianToDegree(theta);
}'Computation Geography' 카테고리의 다른 글
| 10. 점과 선 사이의 거리 (0) | 2023.09.15 |
|---|---|
| 9. Vector Collinear, Corplaner Check (0) | 2023.09.15 |
| 7. 두 점(Point)의 교점 구하기 (0) | 2023.09.13 |
| 6. 면 (Plane) (0) | 2023.09.11 |
| 5. 선 (Line), 선과 선의 교차점 체크하기 (0) | 2023.09.09 |



